UNEDF Research Areas
UNEDF has assembled a team of researchers who represent a wide range of intellectual resources, spanning multiple areas of physics, mathematics, and computer science. The main physics areas of UNEDF are:
In order to ensure the close alignment of the necessary applied mathematics and computer science research with the necessary physics research, partnerships have been formed consisting of computer scientists and mathematicians linked with specific physicists. In each partnership, the mathematician/computer scientist is addressing a research topic in order to remove a specific barrier to progress on the computational/algorithmic physics side.
Ab initio structure and reactions
Ab initio calculations of nuclei and nuclear matter aim to predict their novel features and also underpin the validation of the UNEDF. The basic input is the inter-nucleon interaction, which has both two-body and three-body components. Several interactions already in use satisfy the criterion of accurately fitting the two-nucleon data, and we will use them in the ab initio theory of light nuclei. For ab initio calculations beyond mass 4, there are three well-proven methodologies: Green's Function Monte Carlo (GFMC), the No-Core Shell Model (NCSM), and the Coupled Cluster (CC) method, and we use all three of them. Ab initio calculations are validated by comparison with experimental results (energy levels, transitions, scattering phase shifts and cross-sections) and verified by comparisons among methods. The latter is particularly important when experimental results are not available as in the case of neutron matter, highly unstable nuclei and nuclei in the presence of external fields.
The following figure illustrates the strategy for UNEDF ab initio efforts and connections to other UNEDF activities:
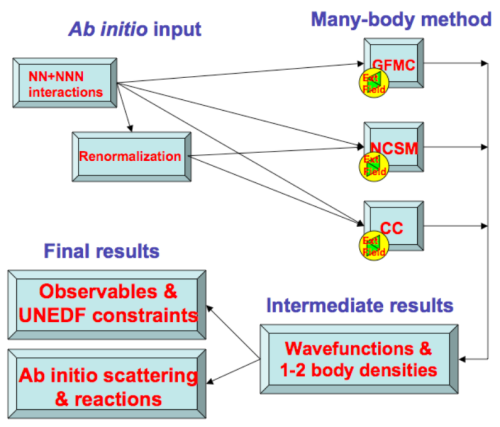
For additional information, see: UNEDF SCIDAC ab initio progress
Density functional theory (DFT) is based on finding the response of the ground-state energy to changes in the density rather than calculating the many-body wave function. This circumvents the computational barriers faced by wave function methods, allowing many (but not all!) important properties of much larger systems to be described. DFT has had widespread success in electronic systems based on energy functionals derived in large part directly from the Coulomb interaction. In contrast, the accurate nuclear energy functionals in use today are purely phenomenological. Renormalization group (RG) evolved nuclear potentials open the door to ab initio (i.e., microscopic) nuclear DFT, because many-body perturbation theory becomes feasible. By combining RG methods with effective field theory (EFT) interactions, ab initio calculations can inform the construction of improved phenomenological functionals with theoretical error bars.
The following figure illustrates
the current UNEDF interconnections and some of the on-going
projects for ab initio
functionals:
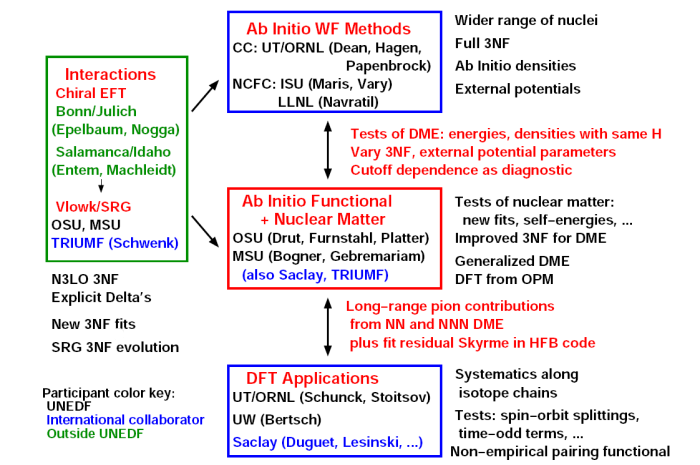Improvements in chiral EFT interactions coupled with advances
in evolving soft low-momentum potentials (Vlowk and
SRG) feed
both into ab initio wave function calculations using coupled
cluster (CC) and no-core full configuration (NCFC) approaches
and into the calculation of ab initio functionals.
The inclusion of three-nucleon forces (3NF) is a particularly important
frontier.
The ab initio functional construction
proceeds either through uniform nuclear matter using some form of
the density matrix expansion (DME),
or by isolating long-range pion contributions and merging them
with phenomenological functionals.
Candidate functionals can then be tested against large-scale CC or NCFC
calculations with the same Hamiltonian, using external potentials
as probes, and against nuclear data systematics
using the DFT Applications machinery.
For additional information, see: Microscopic Input to Energy Functionals
By DFT theory we mean a theory based on an energy functional of orbital variables, such as the well-known Kohn-Sham density functional theory in condensed matter. In practice this approach is identical to the self-consistent mean-field theory, apart from the fact that the EDF has a strong ab initio underpinning, in which the Hamiltonian is modified to take into account correlation effects. Mean-field theory has long been an essential tool for understanding nuclei. From the early days of restricted application to magic nuclei and to the qualitative justification of the phenomenological shell model, the theory blossomed in the 1990s to become a powerful quantitative tool for all aspects of nuclear structure in medium to heavy nuclei. Present self-consistent mean-field theories are much like the EDF theory of condensed matter. We believe we can make an order-of-magnitude improvement in the reliability and accuracy of the theory with another generation of functionals coupled with the high-performance computing that is now available. These improvements are urgently needed for several reasons. EDF theory is the microscopic method of choice for calculating masses and for interpreting data from the upcoming generation of exotic beam facilities. Further, it is the basis of theories of dynamic processes describing fission and low-energy reactions.
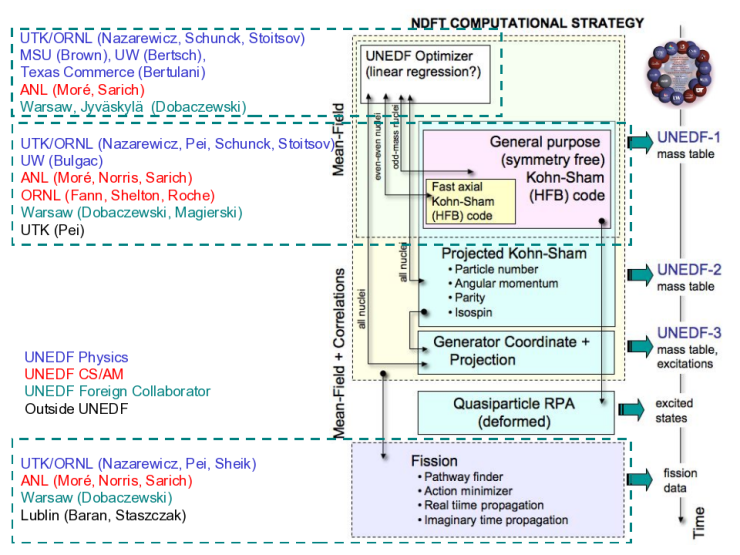
For additional information, see: Using the Functionals: Towards Spectroscopic-Quality NEDF (DFT Applications)
The main goals of this part of UNEDF are: (i) Develop modern computational infrastructure for extending the nuclear DFT to calculate excited states and their associate observables (transition probabilities, level densities, etc); (ii) Investigate the connection between EDF and the Configuration Interaction (CI) Hamiltonians via mapping to Fock space; (iii) Optimize the extensions of EDF to theoretical and experimental data; (iv) Develop technology to estimate theoretical uncertainties, in particular when extrapolating to unknown regions; and (v) Through large-scale calculations guide experimental efforts, and provide input to the UNEDF nuclear reaction group. The general organization of the DFT-Extensions activity and its computational branches are shown in the following figure:
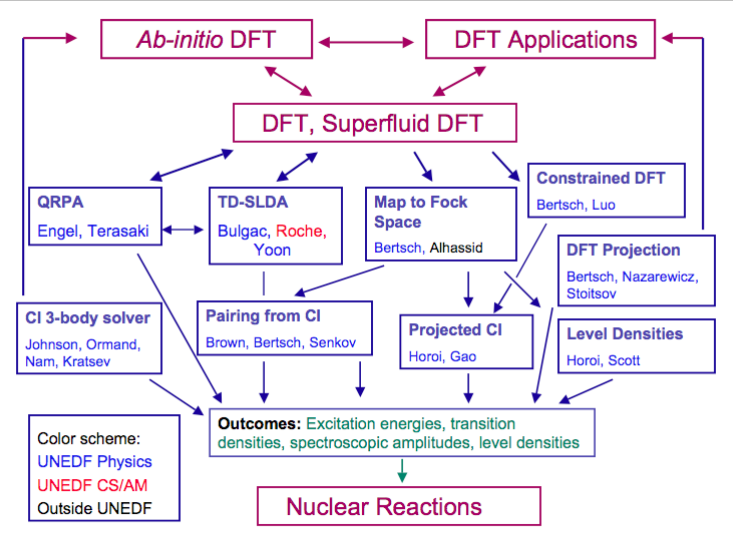
For additional information, see: DFT Extensions for Dynamics, Excited States
The collaboration's nuclear structure results will be used to calculate all the outcomes for incident neutrons or protons reacting on a nucleus. We thereby achieve a microscopic and ab initio calculation of nucleon-nucleus reactions, by explicitly calculating target excitations induced by the incident nucleon. By using the UNEDF microscopic structure models, all rotational, vibration, single-particle, pre-equilibrium and giant-resonance excitations are included on an equal footing. The coupling between structure and reactions will be accomplished in several ways, according to the size of the nucleus and the method of the structure theory: we are using structural Hamiltonian matrix elements directly in ab initio calculations for scattering; using RPA occupation amplitudes for ground and excited states to calculate DWBA matrix elements for neutron emission; or using RPA amplitudes to give the transition potentials for a full coupled-channels calculation of scattering. From the coupled-channels results we extract optical potentials, using statistical methods to average over compound-nucleus resonances for the optical potential. Later we will include transfer channels (pickup to deuteron intermediate states), and we will adapt the density functional itself to give effective interactions between continuum states.
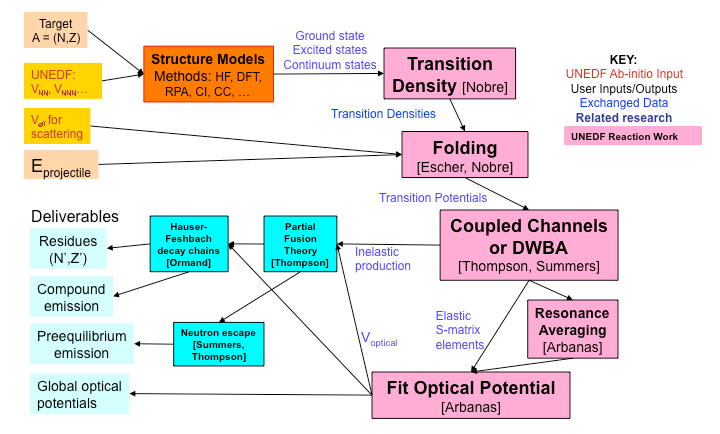
For additional information, see: Reaction Theory in UNEDF Optical Potentials from DFT Models
Computer Science and Applied Mathematics
The Asynchronous Dynamic Load-Balancing Library
Ab initio Calculations of Microscopic Structure of Nuclei
Computational Infrastructure for Nuclear Energy Density Functional Theory